当我们使用前馈神经网络接收输入 \(\boldsymbol{x}\) 并产生输出 \(\hat{\boldsymbol{y}}\) 时,信息通过网络向前流动。输入 \(\boldsymbol{x}\) 提供初始信息,然后传播到每一层的隐藏单元,最终产生输出 \(\hat{\boldsymbol{y}}\) 。这称之为 向前传播 (forward propagation)。在训练过程中,向前传播可以持续向前直到它产生一个标量代价函数 \(J(\boldsymbol{\theta})\) 。 反向传播 (back propagation) 算法允许来自代价函数的信息通过网络向后流动,以便计算梯度。
计算梯度的解析表达式是很直观的,但是数值化地求解这样的表达式在计算上的代价可能很大。反向传播算法使用简单和廉价的程序来实现这个目标。
反向传播仅指用于计算梯度的方法,而另一种算法,例如随机梯度下降,是使用该梯度进行学习。
计算图
计算图 (computational graph) 语言,是将数学计算形式化为图形的方法。有很多这种方法,这里使用途中的每一个节点来表示一个变量,变量可以是标量、向量、矩阵、张量或者是另一类型的变量。
操作是指一个或多个变量的简单函数。图形语言伴随着一组被允许的操作,我们可以通过将多个操作复合在一起来描述更为复杂的函数。
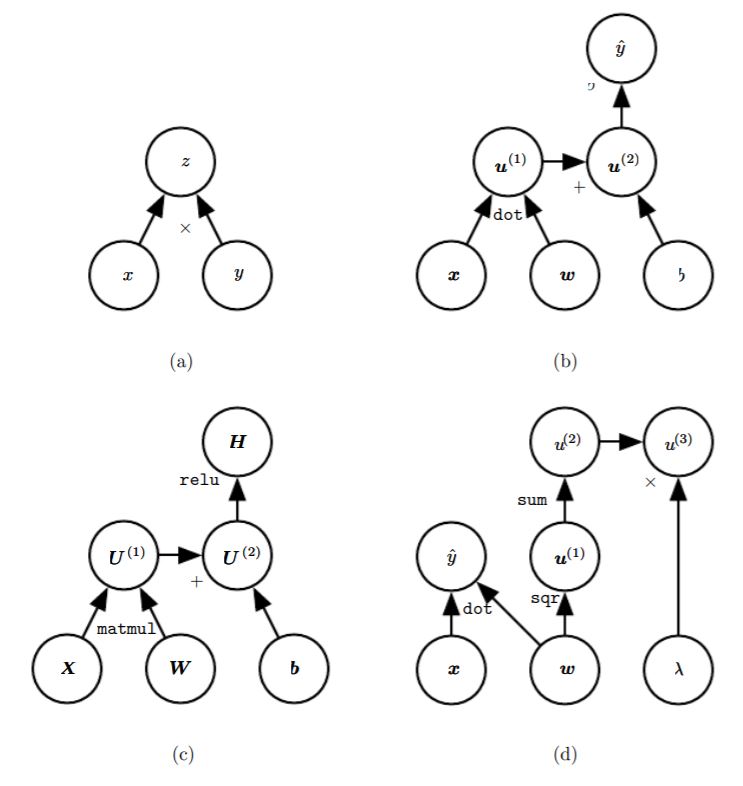
微积分中的链式法则
微积分的链式法则(chain rule)即是微积分中的求导法则,用于求一个复合函数的导数,是在微积分的求导运算中一种常用的方法。参考 Derivative rules
对于标量的情况,设 \(x\) 是实数,\(f\) 和 \(g\) 是从实数映射到实数的函数。假设 \(y=g(x)\) 并且 \(z=f(g(x))=f(y)\)。那么链式法则是指
\[\frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}\]扩展到向量的情况,假设 \(\boldsymbol{x}\in\mathbb{R}^m,\boldsymbol{y}\in\mathbb{R}^n\),\(g\) 是从 \(\mathbb{R}^m\) 到 \(\mathbb{R}^n\) 的映射,\(f\) 是从 \(\mathbb{R}^n\) 到 \(\mathbb{R}\) 的映射。如果 \(\boldsymbol{y}=g(\boldsymbol{x})\) 并且 \(z=f(\boldsymbol{y})\),那么
\[\displaystyle \frac{\partial z}{\partial x_i}=\sum_j\frac{\partial z}{\partial y_j}\frac{\partial y_j}{\partial x_i}\]使用向量记法,可以等价地写成
\[\displaystyle\nabla_\boldsymbol{x}z=\left(\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}}\right)^\top\nabla_\boldsymbol{y}z\]这里 \(\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}}\) 是 \(g\) 的 \(n \times m\) 的 Jacobian 矩阵。
从这里我们看到,变量 \(\boldsymbol{x}\) 的梯度可以通过 Jacobian 矩阵 \(\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}}\) 和梯度 \(\nabla_\boldsymbol{y}z\) 相乘来得到。反向传播算法由计算图中每一个这样的 Jacobian 梯度的乘积操作所组成。
上面说的是标量和向量的反向传播算法,完全可以推广到任何维度的张量上去。
Calculus on Computational Graphs: Backpropagation
http://www.deepideas.net/deep-learning-from-scratch-i-computational-graphs/
多层感知器的反向传播算法
https://blog.csdn.net/qq_32611933/article/details/51612102
https://blog.csdn.net/zhuimeng999/article/details/80795943
多层感知器的监督训练最初是以批量学习和在线学习进行的。
首先将误差函数表示为
\[\displaystyle \mathcal{E}(n) = \frac 1 2 \sum_{j \in C} e_{j}^2(n)\]那么对于训练样本中包含 N 个样例,则误差函数定义为:
\[\displaystyle \mathcal{E}_{av}(N) = \frac 1 {N} \sum_{n=1}^N \mathcal{E}(n) = \frac 1 {2N} \sum_{n=1}^N \sum_{j \in C} e_{j}^2(n)\]其中ej(n)为第n个样本产生的第j个输出值的误差信号,即期望值减去输出值:
\[e_j(n)=d_j(n)-y_j(n)\]\(\mathcal{E}(n)\) 也就是第 n 个样本输入产生的输出层所有的输出的误差的平方和再除以 2 。除以 2 是为了后边求导时可以直接消掉。它也被称为全部瞬时误差能量。
反向传播算法的实现
纯 Python 实现
https://medium.com/@curiousily/tensorflow-for-hackers-part-iv-neural-network-from-scratch-1a4f504dfa8
我们用 Python 和 Numpy 来实现一个简单的神经网络反向传播算法实例,这个简单的神经网络是只是用一层隐藏层解决 XOR 问题
然后我们的神经网络是包含一层隐藏层和一层输出层的简单神经网络,其中隐藏层使用激活函数为 sigmod
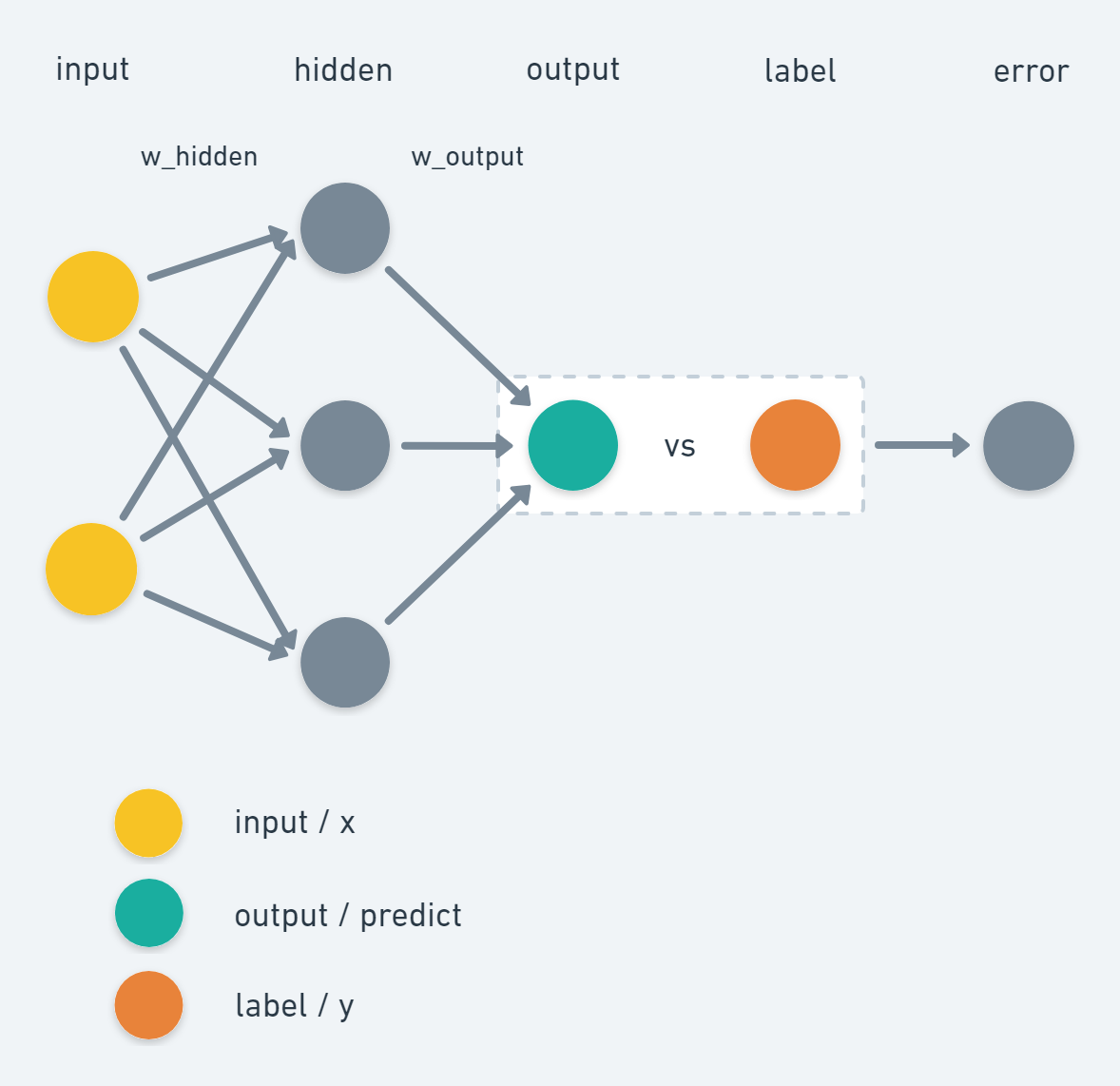
可以看出输入层大小为 2,隐藏层大小为 3,输出层大小为 1,这就作为神经网络的初始参数
# parameters and hyperparameters
epochs = 50000
input_size, hidden_size, output_size = 2, 3, 1
LR = .1 # learning rate
初始化一下我们的训练数据
# Our data: x,y
X = np.array([[0,0], [0,1], [1,0], [1,1]])
y = np.array([ [0], [1], [1], [0]])
开始我们的训练过程,首先用随机数初始化一下权重参数
# Initlize wights
w_hidden = np.random.uniform(size=(input_size, hidden_size))
w_output = np.random.uniform(size=(hidden_size, output_size))
然后就循环地训练模型
# Training
for epoch in range(epochs):
# Forward
act_hidden = sigmoid(np.dot(X, w_hidden))
output = np.dot(act_hidden, w_output)
# Calculate error
error = y - output
if epoch % 5000 == 0:
print(f'error sum {sum(error)}')
# Backward
dZ = error * LR
w_output += act_hidden.T.dot(dZ)
dH = dZ.dot(w_output.T) * sigmoid_prime(act_hidden)
w_hidden += X.T.dot(dH)
其中 sigmoid 和 sigmoid_prime 是我们预定义的函数。
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_prime(x):
return x * (1 - x)
我们要重点看一下 Backward 这段代码的逻辑
TensorFlow 的实现
http://blog.aloni.org/posts/backprop-with-tensorflow/
https://towardsdatascience.com/manual-back-prop-with-tensorflow-decoupled-recurrent-neural-network-modified-nn-from-google-f9c085fe8fae
Comments