• Linear Algebra
  • Matrix
    • 矩阵乘法
    • Linear Dependence and Span
    • Special Kinds of Matrices and Vectors
  • Norms 范数
    • Eigendecomposition 特征分解
  • Tensors
• Statistics
  • Random Variables
  • Probability distributions
    • Expectation
    • Variance
    • Covariance
  • Common Probability Distributions
    • Bernoulli distribution
    • Multinoulli Distribution
    • Gaussian Distribution
    • 分布的混合
  • 常用函数
  • Least Squares
  • Entropy
  • Convolution
• Calculus
  • Derivative
    • Partial derivative
    • Directional derivative
• Machine Learning
  • 学习算法
  • 设计学习算法的基本原则
  • 学习的目标
  • 构建机器学习算法
    • Manifold learning
  • Loss function
    • MSE
  • Gradient Descent
  • Classification and regression
  • Convex function
• 专业词汇

Linear Algebra

• Scalars
• Vectors
• Matrices
• Tensors
• Hyperplanes

关于线性代数非常直观的讲解可以观看 YouTube - 3Blue1Brown - Essence of linear algebra

Matrix

矩阵乘法

• Dot product
• Element-wise product (Hadamard product)
• Outer product

矩阵乘法 (Matrix multiplication) 的结果称为矩阵积 (Matrix product).

矩阵可以用来表示线性映射，矩阵积则可以用来表示线性映射的复合。因此，矩阵乘法是线性代数的基础工具，不仅在数学中有大量应用，在应用数学、物理学、工程学等领域也有广泛使用.

Linear Dependence and Span

• linear dependence 线性相关
• linearly independent 线性无关
• linear combination 线性组合
• span 生成子空间
• singular square 奇异方阵
• matrix inversion 矩阵逆

Special Kinds of Matrices and Vectors

• diagonal matrix 对角矩阵
• symmetric matrix 对称矩阵
• unit vector 单位向量
• unit norm 单位范数
• orthogonal matrix 正交矩阵
• Jacobian matrix

Jacobian matrix

Khan Academy Lessons: Jacobian

Norms 范数

向量的大小成为范数 (Norm), \(L^p\) 的范数定义如下

\[\displaystyle \|x\|_p=(\sum_{i}|x_i|^p)^\frac{1}{p}\]

最大范数 (max norm) 定义为

\[\displaystyle \|x\|_{\infty}=\max_{i}|x_i|\]

衡量矩阵的大小可以用 Frobenius 范数 (Frobenius norm):

\[\displaystyle \|A\|_F=\sqrt{\sum_{i,j}A_{i,j}^2}\]

Eigendecomposition 特征分解

• eigenvector 特征向量
• positive definite 正定
• positive semidefinite 半正定
• negative definite 负定
• negative semidefinite 半负定

线性代码应用实例：主成分分析 (principal components analysis, PCA)

Tensors

Tensor: In mathematics, tensors are geometric objects that describe linear relations between geometric vectors, scalars, and other tensors. Elementary examples of such relations include the dot product, the cross product, and linear maps. Geometric vectors, often used in physics and engineering applications, and scalars themselves are also tensors.

In short, tensor is a mathematical term for n-dimensional arrays. For example, a 1×1 tensor is a scalar, a 1×n tensor is a vector, an n×n tensor is a matrix, and an n×n×n tensor is just a three-dimensional array.

Statistics

• Probabilities
• Distributions
• Likelihood 似然

Bayesian probability (贝叶斯概率) 是由 Bayes’ theorem (贝叶斯理论) 所提供的一种对概率的解释，它采用将概率定义为某人对一个命题信任的程度的概念。贝叶斯理论同时也建议贝叶斯定理可以用作根据新的信息导出或者更新现有的置信度的规则。

Random Variables

On its own, a random variable is just a description of the states that are possible; it must be coupled with a probability distribution that specifies how likely each of these states are.

Probability distributions

At a high level, probabiity distributions provide a mathematical trick that allows you to relax a discrete set of choices into a continuum.

• Probability mass function, PMF 概率质量函数用来描述离散型随机变量的概率的函数，它代表的是变量在某个取值上的概率。
• Probability density function, PDF 概率密度函数用来描述连续型随机变量的概率的函数，它代表的是变量在某个取值上的概率密度，要说概率只能是变量在某个区间上的概率，要通过 PDF 在此区间求积分得到此概率。
• Joint probability distribution 联合概率分布是对多个随机变量如两个随机变量 \(X\) 和 \(Y\) 的概率分布。
• Marginal probability distribution 边缘概率分布是指对于多个变量的联合分布，其中一部分变量（子集）的概率分布。要通过对此子集外的变量函数求和或者积分来计算得到。
• Conditional probability distribution 条件概率分布是指对于多个变量的联合分布，如果指定一部分变量的值的情况下，变量剩下的部分（子集）的概率分布。
• 条件概率的链式法则或者乘法法则，即任何多维随机变量的联合概率分布，都可以分解成只有一个变量的条件概率相乘的形式:
  \(P(x^{(1)},\dots,x^{(n)})=P(x^{(1)})\prod_{i=2}^nP(x^{(i)}|x^{(1)},\dots,x^{(i-1)})\)
• 直觉上是指一次实验中一事件的发生不会影响到另一事件发生的概率，那么称为两个事件的随机变量是独立 (independent) 的，记作\(x \bot y\)。Conditional independence (条件独立)是指在给定随机变量 \(z\) 时两个随机变量\(x\)和\(y\)是独立的，记作 \(x \bot y|z\)。

Expectation

函数 \(f(x)\) 关于（由其影响的）某分布 \(P(x)\) 的期望 (expectation) 或叫期望值 (expected value) 是指，当 \(x\) 由概率分布 \(P\) 产生，\(f\) 作用于 \(x\) 时，\(f(x)\) 的平均值（平均值不平均而是概率均）。 对于离散型随机变量，期望值可以通过求和得到:

\[\displaystyle\mathbb{E}_{x \sim P}[f(x)]=\sum_xP(x)f(x)\]

对于连续型随机变量可以通过求积分得到:

\[\displaystyle\mathbb{E}_{x \sim p}[f(x)]=\int p(x)f(x)dx\]

当你我他都清楚时可以简写为:

\[\mathbb{E}[f(x)]\]

期望是线性的:

\[\mathbb{E}_x[\alpha f(x) + \beta g(x)] = \alpha \mathbb{E}_x[f(x)] + \beta \mathbb{E}_x[g(x)]\]

Variance

方差 (variance) 衡量的是使用概率分布和不使用概率分布的 \(f(x)\) 的差异:

\[Var(f(x)) = \mathbb{E}[(f(x) - \mathbb{E}[f(x)])^2]\]

方差的平方根即为标准差 (standard deviation)

Covariance

协方差 (covariance) 在某种意义上给出了两个变量线性相关性的强度以及这些变量的尺度:

\[Cov(f(x),g(y)) = \mathbb{E}[(f(x) - \mathbb{E}[f(x)])(g(y) - \mathbb{E}[g(y)])]\]

协方差矩阵 (Covariance matrix)

Common Probability Distributions

Bernoulli distribution

Bernoulli distribution 伯努利分布又名两点分布或者0-1分布，是一个离散型概率分布。 它具有如下性质:

\[P(\mathbf{x}=1)=\phi \\ P(\mathbf{x}=0)=1-\phi \\ P(\mathbf{x}=x)=\phi ^x (1-\phi)^{1-x} \\ \mathbb{E}_{\mathbf{x}}[\mathbf{x}]=\phi \\ \mathbf{Var}_{\mathbf{x}}(\mathbf{x})=\phi(1-\phi)\]

Multinoulli Distribution

Multinoulli Distribution 或称 Categorical distribution 范畴分布，它是 Multinomial distribution 多项式分布 \(\{0,\dots,n\}^k\) 的一个特例 (\(n=1\))。

Gaussian Distribution

Normal Distribution 正态分布，也称为 Gaussian Distribution 高斯分布，是实数上最常用的分布。

\[\mathcal{N}(x;\mu,\sigma^2)=\sqrt{\frac{1}{2\pi\sigma^2}}\exp\left(-\frac{1}{2\sigma^2}(x-\mu)^2\right)\]

当 \(\mu=0,\sigma=1\) 时为标准正态分布

\[\mathcal{N}(x)=\sqrt{\frac{1}{2\pi}}\exp\left(-\frac{x^2}{2}\right)\]

正态分布可以推广到 \(\mathbb{R}^n\) 空间，称为 多维正态分布 (multivariate normal distribution)

\[\mathcal{N}(\pmb{x};\pmb{\mu},\pmb{\Sigma})=\sqrt{\frac{1}{(2\pi)^n\det(\pmb{\Sigma})}}\exp\left(-\frac{1}{2}(\pmb{x}-\pmb{\mu})^{\top}\pmb{\Sigma}^{-1}(\pmb{x}-\pmb{\mu})\right)\]

其中 \(\pmb{\Sigma}\) 是一个 正定 对称 矩阵。

正态分布的前世今生

• 指数分布和 Laplace 分布
• Dirac 分布和经验分布

分布的混合

Mixture model (混合模型)是组合简单概率分布来生成更丰富的分布的一种简单策略。一个非常强大且常见的混合模型是 Guassian Mixture Model (高斯混合模型)

Mixture distribution:

\[\displaystyle P(\mathbf{x})=\sum_iP(c=i)P(\mathbf{x}|c=i)\]

这里\(P(c)\)是对各组件的一个 Multinoulli 分布。

常用函数

// TODO

Least Squares

Least Squares

zhihu - 最小二乘法

Entropy

\[y = xlog(x)\]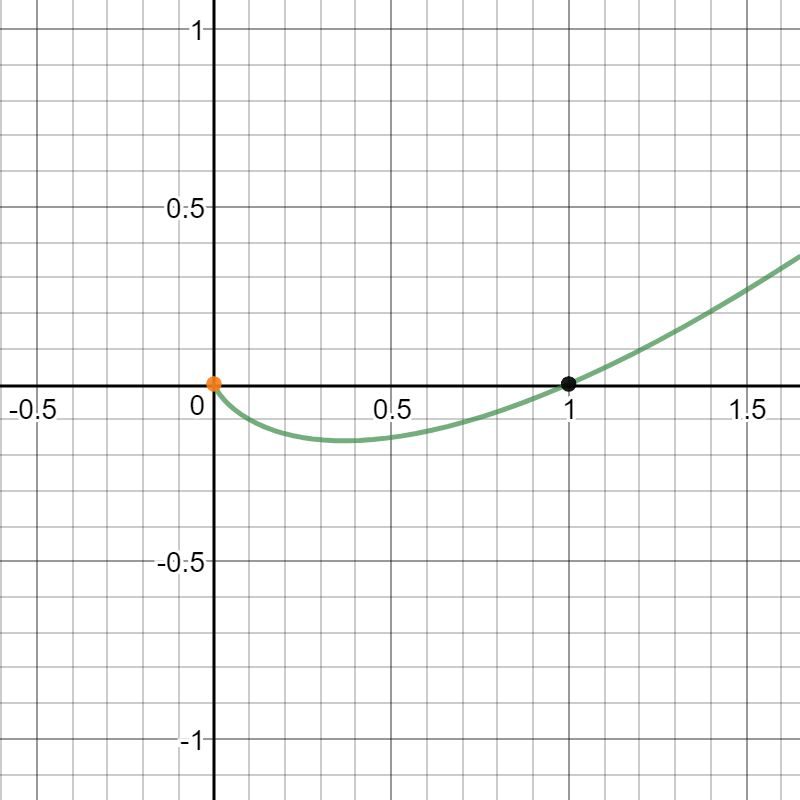

Cross-entropy is a mathematical method for gauging the distance between two probability distributions: Here \(p\) and \(q\) are two probability distributions. the notation \(p(x)\) denotes the probability \(p\) accords to event \(x\). Like the \(L2\) norm, \(H\) provides a notion of distance. Note that in the case where \(p = q\) , this quantity is the entropy of \(p\) and is usually written simply \(H(p)\). It’s a measure of how disorderd the distribution is; The entropy is maximized when all events are equally likely. \(H(p)\) is always less than or equal to \(H(p, q)\). In fact, the “further away” distribution \(q\) is from \(p\), the larger the cross-entropy gets.

\[H(p,q) = -\sum_x p(x)log(q(x))\]

As an aside, note that unlike \(L2\) norm, \(H\) is asymmetric.

Convolution

Convolution 定义

\[(f\ast g)(c) = \sum_a f(a) \cdot g(c-a)\]

Convolution of probability distributions

planetmath - Convolution

Calculus

Calculus

Derivative

导数（英语：Derivative）是微积分学中重要的基础概念。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。导数的本质是通过极限的概念对函数进行局部的线性逼近。当函数 \(f\) 的自变量在一点 \(x_0\) 上产生一个增量 \(h\) 时，函数输出值的增量与自变量增量 \(h\) 的比值在 \(h\) 趋于 0 时的极限如果存在，即为 \(f\) 在 \(x_{0}\) 处的导数，记作 \(f'(x_{0})\) 或 \(\frac{\mathrm{d}f}{\mathrm{d}x}(x_{0})\) 或 \(\left.\frac{\mathrm{d}f}{\mathrm{d}x}\right\| _{x=x_0}\) 导函数公式定义为

\[\displaystyle f'(x_{0}) = \lim_{\Delta x \to 0}\frac{\Delta x}{\Delta y} = \lim_{\Delta x \to 0}\frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}\]

Partial derivative

偏导数 (Partial derivative) 定义为

\[\displaystyle \frac{∂}{∂x_j}f(x_0,x_1,\cdots,x_n) = \lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0}\frac{f(x_0,x_1,\cdots,x_n)-f(x_0,x_1,\cdots,x_n)}{\Delta x}\]

Directional derivative

方向导数 (Directional derivative) 定义为

\[\displaystyle \frac{∂}{∂l}f(x_0,x_1,\cdots,x_n) = \lim_{\rho \to 0}\frac{\Delta y}{\Delta x} = \lim_{\rho \to 0}\frac{f(x_0+\Delta x_0,x_1+\Delta x_1,\cdots,x_n+\Delta x_n)-f(x_0,x_1,\cdots,x_n)}{\rho} \\ \rho = \sqrt{(\Delta x_0)^2+(\Delta x_1)^2+\cdots+(\Delta x_n)^2}\]

Machine Learning

At a very high level, machine learning is simply the act of function minimization: learning algorithms are nothing more than minima finders for suitably defined functions.

超参数 必须在学习算法外设定。机器学习本质上属于应用统计学，频率派估计 和 贝叶斯推断，监督学习 和 无监督学习，generalize (泛化)

学习算法

Learning 学习：“对于某类任务\(T\)和性能度量\(P\)，一个计算机程序被认为可以从经验\(E\)中学习是指，通过经验\(E\)改进后，它在任务\(T\)上由性能度量\(P\)衡量的性能有所提升。”

example (样本) 表示为向量 \(\pmb{x} \in \mathbb{R}^n\), feature (特征) 是向量的一个元素 \(x_i\)

任务:

• Classification 分类
• Classification with missing inputs 输入缺失分类
• Regression
• Transcription
• Machine translation
• Structured output
• Anomaly detection
• Synthesis and sampling
• Imputation of missing values
• Denoising
• Density estimation or probability mass function estimation

对于任务结果属于离散型的模型通常度量其 accuracy (准确率，反面为 errorrate 错误率) 来衡量其性能。而结果为连续型变量的任务，常用的方式是输出模型在一些样本上的概率对数的平均值。

机器学习算法可以大致分类为 unsupervised (无监督) 算法和 supervised (监督) 算法。

传统上，人们将回归、分类或者结构化输出问题称为监督学习，将支持其他任务的密度估计称为无监督学习。

表示数据集的常用方法是 design matrix (设计矩阵)，每一行包含一个不同的样本，每一列对应不同的特征。

度量模型性能的一种方法是计算模型在测试集上的 mean squared error (均方误差)

设计学习算法的基本原则

在先前未观测到的输入上表现良好的能力被称为 generalization (泛化)

training error (训练误差) test error (测试误差)

underfitting (欠拟合) 是指模型不能在训练集上获得足够低的误差，overfitting (过拟合) 是指训练误差和测试误差之间的差距过大。通过调整模型的 capacity (容量) 可以控制模型是否偏向于过拟合或者欠拟合。

Regularization (正则化) 是指修改学习算法，使其降低泛化误差而非训练误差，正则化是机器学习领域的中心问题之一，只有优化能够与其重要性相提并论。

hyperparameters (超参数) 是指学习算法能学习的参数之外的参数，为什么有学习之外的参数，因为它太难优化了，尽管可以设计一个嵌套的学习过程。

用于挑选超参数的数据子集被称为 validation set (验证集)

学习的目标

Point estimation (点估计) 是用样本统计量来估计总体参数，因为样本统计量为数轴上某一点值，估计的结果也以一个点的数值表示，所以称为点估计。点估计和区间估计属于总体参数估计问题。何为总体参数统计，当在研究中从样本获得一组数据后，如何通过这组信息，对总体特征进行估计，也就是如何从局部结果推论总体的情况，称为总体参数估计。

为了区分参数估计和真实值，将参数 \(\boldsymbol{\theta}\) 的点估计表示为 \(\hat{\boldsymbol{\theta}}\) 。令 \(\{x^{(1)},\dots,x^{(m)}\}\) 是 \(m\) 个独立同分布的数据点。点估计是这些数据的任意函数:

\[\hat{\boldsymbol{\theta}}_m=g(\boldsymbol{x}^{(1)},\dots,\boldsymbol{x}^{(m)})\]

点估计也可以指输入和目标变量之间关系的估计，我们将这种类型的点估计称为函数估计。

估计的偏差定义为

\[bias(\hat{\boldsymbol{\theta}}_m)=\mathbb{E}(\hat{\boldsymbol{\theta}}_m)-\boldsymbol{\theta}\]

如果 \(\displaystyle \lim_{m\rightarrow\infty} bias(\hat{\boldsymbol{\theta}}_m)=0\) 那么估计量 \(\hat{\boldsymbol{\theta}}_m\) 被称为是 asymptotically unbiased (渐近无偏)，这意味着 \(\displaystyle \lim_{m\rightarrow\infty} \mathbb{E}(\hat{\boldsymbol{\theta}}_m)=\boldsymbol{\theta}\)

偏差和方差度量着估计量的两个不同误差来源。偏差度量这偏离真实函数或者参数的误差期望，而方差度量着数据上任意特定采样可能导致的估计期望的偏差。

Maximum likelihood estimation (最大似然估计)

CSDN - 极大似然估计详解

构建机器学习算法

深度学习算法的简单配方：特定的数据集、代价函数、优化过程和模型。

Closed-form expression (解析解)，又称为闭式解，是可以用解析表达式来表达的解。 在数学上，如果一个方程或者方程组存在的某些解，是由有限次常见运算的组合给出的形式，则称该方程存在解析解。当解析解不存在时，比如五次以及更高次的代数方程，则该方程只能用数值分析的方法求解近似值 (数值解)。

Manifold learning

Manifold learning

http://scikit-learn.org/stable/modules/manifold.html

https://jakevdp.github.io/PythonDataScienceHandbook/05.10-manifold-learning.html

Loss function

损失函数 (Loss function)

All of machine learning, and much of artificial intelligence, boils down to the creation of the right loss function to solve the problem at hand.

• Cross Entropy

MSE

L1 L2 loss functions

MSE (Mean squared error)

Why Mean Squared Error and L2 regularization? A probabilistic justification

Gradient Descent

梯度下降法 (Gradient Descent)

Classification and regression

Machine learning algorithms can be broadly categorized as supervised or unsupervised problems. Supervised problems are those for which both datapoints \(x\) and labels \(y\) are available, while unsupervised problems have only datapoints \(x\) without labels \(y\).

Supervised machine learning can be broken up into the two subproblems of classification and regression.

Convex function

凸函数 (Convex function)

专业词汇

• approximation
• continuous function approximation
• numerical 数值
• numerical analysis 数值分析